HDU 4069 Squiggly Sudoku （精确覆盖 Dancing Links）

HDU4069

变形的数独问题，就是Dancing Links 的精确覆盖模板题了。 题目：

Squiggly Sudoku

Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 1420 Accepted Submission(s): 588

Problem Description

Today we play a squiggly sudoku, The objective is to fill a 9*9 grid with digits so that each column, each row, and each of the nine Connecting-sub-grids that compose the grid contains all of the digits from 1 to 9. Left figure is the puzzle and right figure is one solution.

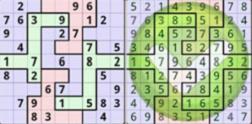
Now, give you the information of the puzzle, please tell me is there no solution or multiple solution or one solution.

Input

The first line is a number T(1<=T<=2500), represents the number of case. The next T blocks follow each indicates a case. Each case contains nine lines, Each line contains nine integers. Each module number tells the information of the gird and is the sum of up to five integers: 0~9: ‘0’ means this gird is empty, ‘1’ - ‘9’ means the gird is already filled in. 16: wall to the up 32: wall to the right 64: wall to the down 128: wall to the left I promise there must be nine Connecting-sub-grids, and each contains nine girds.

Output

For each case, if there are Multiple Solutions or no solution just output “Multiple Solutions” or “No solution”. Else output the exclusive solution.(as shown in the sample output)

Sample Input

3
144 18 112 208 80 25 54 144 48
135 38 147 80 121 128 97 130 32
137 32 160 144 114 167 208 0 32
192 100 160 160 208 96 183 192 101
209 80 39 192 86 48 136 80 114
152 48 226 144 112 160 160 149 48
128 0 112 166 215 96 160 128 41
128 39 153 32 209 80 101 136 35
192 96 200 67 80 112 208 68 96

144 48 144 81 81 16 53 144 48
128 96 224 144 48 128 103 128 38
163 208 80 0 37 224 209 0 32
135 48 176 192 64 112 176 192 104
192 101 128 89 80 82 32 150 48
149 48 224 208 16 48 224 192 33
128 0 114 176 135 0 80 112 169
137 32 148 32 192 96 176 144 32
192 96 193 64 80 80 96 192 96

144 88 48 217 16 16 80 112 176
224 176 129 48 128 40 208 16 37
145 32 128 96 196 96 176 136 32
192 32 227 176 144 80 96 192 32
176 192 80 98 160 145 80 48 224
128 48 144 80 96 224 183 128 48
128 36 224 144 51 144 32 128 105
131 64 112 136 32 192 36 224 176
224 208 80 64 64 116 192 83 96

Sample Output

Case 1:
521439678
763895124
984527361
346182795
157964832
812743956
235678419
479216583
698351247
Case 2:
No solution
Case 3:
Multiple Solutions

Source

The 36th ACM/ICPC Asia Regional Fuzhou Site —— Online Contest

和普通数独不一样的就是 分小块不一样， bfs一下就可以了。   此题要判断是唯一解 、还是多解、还是无解。   代码：  

/* ***************

Author        :kuangbin

Created Time  :2014/5/31 12:05:46

File Name     :E:\2014ACM\专题学习\DLX\HDU4069.cpp

************************************************ */

#include <stdio.h>

#include <string.h>

#include <iostream>

#include <algorithm>

#include <vector>

#include <queue>

#include <set>

#include <map>

#include <string>

#include <math.h>

#include <stdlib.h>

#include <time.h>

using namespace std;

const int N = 9; //3*3数独

const int MaxN = N*N*N + 10;

const int MaxM = N*N*4 + 10;

const int maxnode = MaxN*4 + MaxM + 10;

char g[MaxN];

int cnt;

struct DLX

{

	int n,m,size;

	int U[maxnode],D[maxnode],R[maxnode],L[maxnode],Row[maxnode],Col[maxnode];

	int H[MaxN],S[MaxM];

	int ansd,ans[MaxN];

	void init(int _n,int _m)

	{

		n = _n;

		m = _m;

		for(int i = 0;i <= m;i++)

		{

			S[i] = 0;

			U[i] = D[i] = i;

			L[i] = i-1;

			R[i] = i+1;

		}

		R[m] = 0; L[0] = m;

		size = m;

		for(int i = 1;i <= n;i++)H[i] = -1;

	}

	void Link(int r,int c)

	{

		++S[Col[++size]=c];

		Row[size] = r;

		D[size] = D[c];

		U[D[c]] = size;

		U[size] = c;

		D[c] = size;

		if(H[r] < 0)H[r] = L[size] = R[size] = size;

		else

		{

			R[size] = R[H[r]];

			L[R[H[r]]] = size;

			L[size] = H[r];

			R[H[r]] = size;

		}

	}

	void remove(int c)

	{

		L[R[c]] = L[c]; R[L[c]] = R[c];

		for(int i = D[c];i != c;i = D[i])

			for(int j = R[i];j != i;j = R[j])

			{

				U[D[j]] = U[j];

				D[U[j]] = D[j];

				--S[Col[j]];

			}

	}

	void resume(int c)

	{

		for(int i = U[c];i != c;i = U[i])

			for(int j = L[i];j != i;j = L[j])

				++S[Col[U[D[j]]=D[U[j]]=j]];

		L[R[c]] = R[L[c]] = c;

	}

	void Dance(int d)

	{

		if(cnt > 1)return;

		if(R[0] == 0)

		{

			for(int i = 0;i < d;i++)g[(ans[i]-1)/9] = (ans[i]-1)%9 + '1';

			cnt++;

			return;

		}

		int c = R[0];

		for(int i = R[0];i != 0;i = R[i])

			if(S[i] < S[c])

				c = i;

		remove(c);

		for(int i = D[c];i != c;i = D[i])

		{

			ans[d] = Row[i];

			for(int j = R[i];j != i;j = R[j])remove(Col[j]);

			Dance(d+1);

			if(cnt > 1)return;

			for(int j = L[i];j != i;j = L[j])resume(Col[j]);

		}

		resume(c);

	}

};

int id[20][20];

int a[20][20];

void bfs(int sx,int sy,int d)

{

	queue<pair<int,int> >q;

	q.push(make_pair(sx,sy));

	id[sx][sy] = d;

	while(!q.empty())

	{

		pair<int,int> tmp = q.front();

		int x = tmp.first;

		int y = tmp.second;

		q.pop();

		if(x > 0 && ((a[x][y]%32)/16) == 0)

			if(id[x-1][y] == -1)

			{

				id[x-1][y] = d;

				q.push(make_pair(x-1,y));

			}

		if(x < N-1 && ((a[x][y]%128)/64) == 0)

			if(id[x+1][y] == -1)

			{

				id[x+1][y] = d;

				q.push(make_pair(x+1,y));

			}

		if(y > 0 && ((a[x][y])/128) == 0)

			if(id[x][y-1] == -1)

			{

				id[x][y-1] = d;

				q.push(make_pair(x,y-1));

			}

		if(y < N-1 && ((a[x][y]%64)/32) == 0)

			if(id[x][y+1] == -1)

			{

				id[x][y+1] = d;

				q.push(make_pair(x,y+1));

			}

	}

}

DLX dlx;

int main()

{

    //freopen("in.txt","r",stdin);

    //freopen("out.txt","w",stdout);

	int T;

	scanf("%d",&T);

	int iCase = 0;

	while(T--)

	{

		iCase++;

		for(int i = 0;i < N;i++)

			for(int j = 0;j < N;j++)

				scanf("%d",&a[i][j]);

		memset(id,-1,sizeof(id));

		int index = 0;

		for(int i = 0;i < N;i++)

			for(int j = 0;j < N;j++)

				if(id[i][j] == -1)

					bfs(i,j,++index);

		dlx.init(N*N*N,N*N*4);

		for(int i = 0;i < N;i++)

			for(int j = 0;j < N;j++)

				for(int k = 1;k <= N;k++)

				{

					if(a[i][j]%16 != 0 && a[i][j]%16 != k)continue;

					int r = (i*N+j)*N + k;

					int c1 = i*N+j+1;

					int c2 = N*N+i*N+k;

					int c3 = N*N*2+j*N+k;

					int c4 = N*N*3+(id[i][j]-1)*N+k;

					dlx.Link(r,c1);

					dlx.Link(r,c2);

					dlx.Link(r,c3);

					dlx.Link(r,c4);

				}

		cnt = 0;

		dlx.Dance(0);

		printf("Case %d:\n",iCase);

		if(cnt == 0)printf("No solution\n");

		else if(cnt > 1)printf("Multiple Solutions\n");

		else

		{

			for(int i = 0;i < N*N;i++)

			{

				printf("%c",g[i]);

				if(i % N == N - 1)

					printf("\n");

			}

		}

	}

    return 0;

}