HDU 4921

Map

Time Limit: 3000/1500 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others) Total Submission(s): 92 Accepted Submission(s): 19

Problem Description

There are N pieces of fragments, and we’re going to select some of them to form a map. Some fragments can be selected into the map directly (named 1-level fragments), while each of the rest follows exactly one fragment as its prior fragment. If B follows A and A is an i-level fragment, then B is defined as an (i + 1) - level fragment, and B can be selected only if A has been selected before. Besides, a fragment is followed by at most one other fragment. Each fragment is assigned with a reliability. The reliability of the whole map is sum up by two parts: 1.The sum of reliabilities of all selected fragments; 2.If there are xi i-level fragments in total and we select yi(yi > 1) fragments among them to form the map, the reliability would increase by 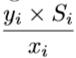,where Sidenotes the sum of reliabilities of selected fragments in level i. Please figure out the expectation of reliability of the map under the condition that all valid selections are equiprobable. At least one fragment should be selected.

Input

There are several test cases. The number of test cases T (T<=10) occurs in the first line of input. For each test case: The first line consists of two integers N, M (1<=N<=10000,0<=M<N), indicating the number of fragments and relationships respectively. The second line contains N integers, which describes the reliability of each fragment. The given reliability ranges from 1 to 100, inclusive. Each of the following M lines contains two integers A and B, which denotes B follows A(0<=A,B<=N-1). You may assume that the number of 1-level fragments are no more than 10, and levels will not exceed 1000. No fragment will follow itself directly or indirectly.

Output

For each test case, output the expectation with 3 decimal places.

Sample Input

2 2 0 1 2 3 1 1 2 4 1 2

Sample Output

3.000 5.000

Hint

In the first sample, there’re three ways of selections: {0,1}, {0},{1},which respectively generates 6, 1 and 2 of reliability. Hence, the expectation is 3.

Source

2014 Multi-University Training Contest 6

大水题一个。 就按照题目说的就是暴力。   卧槽，做的时候没有看到下标从0开始的，一直搞不出来第二个样例，然后WA无数次。  一直没发现问题。 经岐哥提醒是下标从0开始的，然后秒过啊。 sad, 最近这状态是有多差啊，题都做不出来了。   按照题目意思是形成很多条链。 链最多是10条，深度最多1000. 直接暴力。   首先先求出总数，假设有k个链，每条链深度是 num\[k\]. 那么总数就是  num\[1\]\*num\[2\]\*........num\[k\]   - 1了。 先累加第一种和。 只需要扫一遍每条链。 其实就是找出每个点出现的次数，是很好求的。   第二种也是很好求的，直接枚举，二进制去枚举2^k复杂度。 就是按照深度去找，枚举每个深度有几个是达到这个深度的，当然有的是达不到这个深度的。

#include <stdio.h>

#include

#include <string.h>

#include

#include <math.h>
using namespace std;
const int MAXN = 100010;
int to[MAXN];
int rto[MAXN];
bool f[MAXN];

int a[MAXN];
int num[MAXN];
int b[MAXN];
int dep[MAXN];
int two[20];

int main()
{
//freopen(“in.txt”,”r”,stdin);
//freopen(“out.txt”,”w”,stdout);
int T;
int n,m;
scanf(“%d”,&T);
two[0] = 1;
for(int i = 1;i < 20;i++)
two[i] = 2two[i-1];
while(T–)
{
scanf(“%d%d”,&n,&m);
for(int i = 1;i <= n;i++)
scanf(“%d”,&a[i]);
for(int i = 1;i <= n;i++)
{
f[i] = true;
num[i] = 0;
to[i] = -1;
rto[i] = -1;
}
int u,v;
while(m–)
{
scanf(“%d%d”,&u,&v);
u++;
v++;
to[u] = v;
rto[v] = u;
f[v] = false;
}
for(int i = 1;i <= n;i++)
if(to[i] == -1)
{
u = i;
num[u] = 1;
while(rto[u] != -1)
{
num[rto[u]] = num[u]+1;
u = rto[u];
}
}
double tot = 1;
for(int i = 1;i <= n;i++)
if(f[i])
tot = (num[i]+1);
double ans = 0;
int cc = 0;
for(int i = 1;i <= n;i++)
if(f[i])
b[cc++] = i;
for(int i = 0;i < cc;i++)
{
u = b[i];
dep[u] = 1;
double tt = 1.0/(num[u]+1);
double s = 0;
while(1)
{
s += a[u];
ans += s*tt*(tot/(tot-1));//累加第一种
if(to[u] == -1)break;
dep[to[u]] = dep[u] + 1;
num[to[u]] = num[u];
u = to[u];
}
}
int MD = 0;//最大深度
for(int i = 1;i <= n;i++)
MD = max(MD,dep[i]);
for(int d = 1;d <= MD;d++)
{
for(int i = 1;i < two[cc];i++)
{
bool flag = true;
double tt = 1;
int cnt = 0;
double ss = 0;
for(int j = 0;j < cc;j++)
if(i & two[j])
{
cnt++;
ss += a[b[j]];
if(dep[b[j]] != d)
{
flag = false;
break;
}
tt = (num[b[j]]-d+1);
}
else
{
if(dep[b[j]] == d)tt = (dep[b[j]]);
else tt = (dep[b[j]]+1);
}
int cnt2 = 0;
for(int j = 0;j < cc;j++)
if(dep[b[j]] == d)
cnt2++;
if(!flag)continue;
if(cnt > 1)ans += ss\cnt/cnt2*(tt/(tot-1));//累加第二种
}
for(int i = 0;i < cc;i++)
if( to[b[i]] != -1)
b[i] = to[b[i]];
}
printf(“%.3lf\n”,ans);
}
return 0;
}