HDU 3662 3D Convex Hull （三维凸包，求凸包多边形个数）

HDU3662 用来测试模板的，直接三维凸包，求凸包上的多边形个数。

3D Convex Hull

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 1259 Accepted Submission(s): 652

Problem Description

There are N points in 3D-space which make up a 3D-Convex hull*. How many faces does the 3D-convexhull have? It is guaranteed that all the points are not in the same plane.

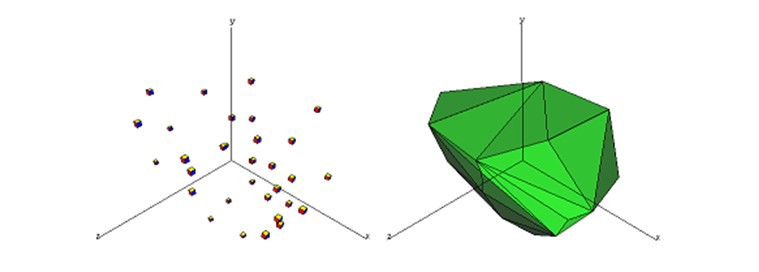
In case you don’t know the definition of convex hull, here we give you a clarification from Wikipedia: *Convex hull: In mathematics, the convex hull, for a set of points X in a real vector space V, is the minimal convex set containing X.

Input

There are several test cases. In each case the first line contains an integer N indicates the number of 3D-points (3< N <= 300), and then N lines follow, each line contains three numbers x, y, z (between -10000 and 10000) indicate the 3d-position of a point.

Output

Output the number of faces of the 3D-Convex hull.

Sample Input

7 1 1 0 1 -1 0 -1 1 0 -1 -1 0 0 0 1 0 0 0 0 0 -0.1 7 1 1 0 1 -1 0 -1 1 0 -1 -1 0 0 0 1 0 0 0 0 0 0.1

Sample Output

8 5

Source

2010 Asia Regional Harbin

/* ***************

Author        :kuangbin

Created Time  :2014/10/7 12:16:51

File Name     :E:\2014ACM\专题学习\计算几何\三维几何\HDU3662.cpp

************************************************ */

#include <stdio.h>

#include <string.h>

#include <iostream>

#include <algorithm>

#include <vector>

#include <queue>

#include <set>

#include <map>

#include <string>

#include <math.h>

#include <stdlib.h>

#include <time.h>

using namespace std;

const double eps = 1e-8;

const int MAXN = 550;

int sgn(double x){

	if(fabs(x) < eps)return 0;

	if(x < 0)return -1;

	else return 1;

}

struct Point3{

	double x,y,z;

	Point3(double _x = 0, double _y = 0, double _z = 0){

		x = _x;

		y = _y;

		z = _z;

	}

	void input(){

		scanf("%lf%lf%lf",&x,&y,&z);

	}

	bool operator ==(const Point3 &b)const{

		return sgn(x-b.x) == 0 && sgn(y-b.y) == 0 && sgn(z-b.z) == 0;

	}

	double len(){

		return sqrt(x*x+y*y+z*z);

	}

	double len2(){

		return x*x+y*y+z*z;

	}

	double distance(const Point3 &b)const{

		return sqrt((x-b.x)(x-b.x)+(y-b.y)(y-b.y)+(z-b.z)*(z-b.z));

	}

	Point3 operator -(const Point3 &b)const{

		return Point3(x-b.x,y-b.y,z-b.z);

	}

	Point3 operator +(const Point3 &b)const{

		return Point3(x+b.x,y+b.y,z+b.z);

	}

	Point3 operator *(const double &k)const{

		return Point3(x*k,y*k,z*k);

	}

	Point3 operator /(const double &k)const{

		return Point3(x/k,y/k,z/k);

	}

	//点乘

	double operator *(const Point3 &b)const{

		return x*b.x + y*b.y + z*b.z;

	}

	//叉乘

	Point3 operator ^(const Point3 &b)const{

		return Point3(y*b.z-z*b.y,z*b.x-x*b.z,x*b.y-y*b.x);

	}

};

struct CH3D{

	struct face{

		//表示凸包一个面上的三个点的编号

		int a,b,c;

		//表示该面是否属于最终的凸包上的面

		bool ok;

	};

	//初始顶点数

	int n;

	Point3 P[MAXN];

	//凸包表面的三角形数

	int num;

	//凸包表面的三角形

	face F[8*MAXN];

	int g[MAXN][MAXN];

	//叉乘

	Point3 cross(const Point3 &a,const Point3 &b,const Point3 &c){

		return (b-a)^(c-a);

	}

	//三角形面积*2

	double area(Point3 a,Point3 b,Point3 c){

		return ((b-a)^(c-a)).len();

	}

	//四面体有向面积*6

	double volume(Point3 a,Point3 b,Point3 c,Point3 d){

		return ((b-a)^(c-a))*(d-a);

	}

	//正：点在面同向

	double dblcmp(Point3 &p,face &f){

		Point3 p1 = P[f.b] - P[f.a];

		Point3 p2 = P[f.c] - P[f.a];

		Point3 p3 = p - P[f.a];

		return (p1^p2)*p3;

	}

	void deal(int p,int a,int b){

		int f = g[a][b];

		face add;

		if(F[f].ok){

			if(dblcmp(P[p],F[f]) > eps)

				dfs(p,f);

			else {

				add.a = b;

				add.b = a;

				add.c = p;

				add.ok = true;

				g[p][b] = g[a][p] = g[b][a] = num;

				F[num++] = add;

			}

		}

	}

	//递归搜索所有应该从凸包内删除的面

	void dfs(int p,int now){

		F[now].ok = false;

		deal(p,F[now].b,F[now].a);

		deal(p,F[now].c,F[now].b);

		deal(p,F[now].a,F[now].c);

	}

	bool same(int s,int t){

		Point3 &a = P[F[s].a];

		Point3 &b = P[F[s].b];

		Point3 &c = P[F[s].c];

		return fabs(volume(a,b,c,P[F[t].a])) < eps &&

			fabs(volume(a,b,c,P[F[t].b])) < eps &&

			fabs(volume(a,b,c,P[F[t].c])) < eps;

	}

	//构建三维凸包

	void create(){

		num = 0;

		face add;

    	//***********************************
    	//此段是为了保证前四个点不共面
    	bool flag = true;
    	for(int i = 1;i < n;i++){
    		if(!(P\[0\] == P\[i\])){
    			swap(P\[1\],P\[i\]);
    			flag = false;
    			break;
    		}
    	}
    	if(flag)return;
    	flag = true;
    	for(int i = 2;i < n;i++){
    		if( ((P\[1\]-P\[0\])^(P\[i\]-P\[0\])).len() > eps ){
    			swap(P\[2\],P\[i\]);
    			flag = false;
    			break;
    		}
    	}
    	if(flag)return;
    	flag = true;
    	for(int i = 3;i < n;i++){
    		if(fabs( ((P\[1\]-P\[0\])^(P\[2\]-P\[0\]))*(P\[i\]-P\[0\]) ) > eps){
    			swap(P\[3\],P\[i\]);
    			flag = false;
    			break;
    		}
    	}
    	if(flag)return;
    	//**********************************
    
    	for(int i = 0;i < 4;i++){
    		add.a = (i+1)%4;
    		add.b = (i+2)%4;
    		add.c = (i+3)%4;
    		add.ok = true;
    		if(dblcmp(P\[i\],add) > 0)swap(add.b,add.c);
    		g\[add.a\]\[add.b\] = g\[add.b\]\[add.c\] = g\[add.c\]\[add.a\] = num;
    		F\[num++\] = add;
    	}
    	for(int i = 4;i < n;i++)
    		for(int j = 0;j < num;j++)
    			if(F\[j\].ok && dblcmp(P\[i\],F\[j\]) > eps){
    				dfs(i,j);
    				break;
    			}
    	int tmp = num;
    	num = 0;
    	for(int i = 0;i < tmp;i++)
    		if(F\[i\].ok)
    			F\[num++\] = F\[i\];
    }
    //表面积
    double area(){
    	double res = 0;
    	if(n == 3){
    		Point3 p = cross(P\[0\],P\[1\],P\[2\]);
    		return p.len()/2;
    	}
    	for(int i = 0;i < num;i++)
    		res += area(P\[F\[i\].a\],P\[F\[i\].b\],P\[F\[i\].c\]);
    	return res/2.0;
    }
    double volume(){
    	double res = 0;
    	Point3 tmp = Point3(0,0,0);
    	for(int i = 0;i < num;i++)
    		res += volume(tmp,P\[F\[i\].a\],P\[F\[i\].b\],P\[F\[i\].c\]);
    	return fabs(res/6);
    }
    //表面三角形个数
    int triangle(){
    	return num;
    }
    //表面多边形个数
    int polygon(){
    	int res = 0;
    	for(int i = 0;i < num;i++){
    		bool flag = true;
    		for(int j = 0;j < i;j++)
    			if(same(i,j)){
    				flag = 0;
    				break;
    			}
    		res += flag;
    	}
    	return res;
    }
    //重心
    Point3 barycenter(){
    	Point3 ans = Point3(0,0,0);
    	Point3 o = Point3(0,0,0);
    	double all = 0;
    	for(int i = 0;i < num;i++){
    		double vol = volume(o,P\[F\[i\].a\],P\[F\[i\].b\],P\[F\[i\].c\]);
    		ans = ans + (((o+P\[F\[i\].a\]+P\[F\[i\].b\]+P\[F\[i\].c\])/4.0)*vol);
    		all += vol;
    	}
    	ans = ans/all;
    	return ans;
    }
    //点到面的距离
    double ptoface(Point3 p,int i){
    	double tmp1 = fabs(volume(P\[F\[i\].a\],P\[F\[i\].b\],P\[F\[i\].c\],p));
    	double tmp2 = ((P\[F\[i\].b\]-P\[F\[i\].a\])^(P\[F\[i\].c\]-P\[F\[i\].a\])).len();
    	return tmp1/tmp2;
    }

};

CH3D hull;

int main()

{

    //freopen("in.txt","r",stdin);

    //freopen("out.txt","w",stdout);

    while(scanf("%d",&hull.n) == 1){

		for(int i = 0;i < hull.n;i++)hull.P[i].input();

		hull.create();

		printf("%d\n",hull.polygon());

	}

    return 0;

}