记录下网络赛写的代码～题目链接： hdu5486

Difference of Clustering

Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 321 Accepted Submission(s): 113

Problem Description

Given two clustering algorithms, the old and the new, you want to find the difference between their results. A clustering algorithm takes many memberentities as input and partition them into clusters. In this problem, a member entity must be clustered into exactly one cluster. However, we don’t have any pre-knowledge of the clusters, so different algorithms may produce different number of clusters as well as different cluster IDs. One thing we are sure about is that the memberIDs are stable, which means that the same member ID across different algorithms indicates the same member entity. To compare two clustering algorithms, we care about three kinds of relationship between the old clusters and the new clusters: split, merge and 1:1. Please refer to the figure below.

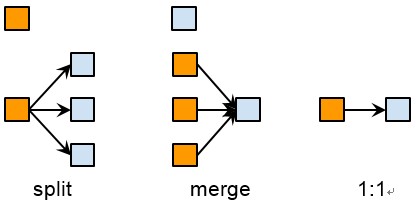
Let’s explain them with examples. Say in the old result, m0, m1, m2 are clustered into one cluster c0, but in the new result, m0 and m1 are clustered into c0, but m2 alone is clustered into c1. We denote the relationship like the following: ● In the old, c0 = [m0, m1, m2] ● In the new, c0 = [m0, m1], c1 = [m2] There is no other members in the new c0 and c1. Then we say the old c0 is split into new c0 and new c1. A few more examples: ● In the old, c0 = [m0, m1, m2] ● In the new, c0 = [m0, m1, m2]. This is 1:1. ● In the old, c0 = [m0, m1], c1 = [m2] ● In the new, c0 = [m0, m1, m2] This is merge. Please note, besides these relationship, there is another kind called “n:n”: ● In the old, c0 = [m0, m1], c1 = [m2, m3] ● In the new, c0 = [m0, m1, m2], c1 = [m3] We don’t care about n:n. In this problem, we will give you two sets of clustering results, each describing the old and the new. We want to know the total number of splits, merges, and 1:1 respectively.

Input

The first line of input contains a number T indicating the number of test cases (T≤100). Each test case starts with a line containing an integer N indicating the number of member entities (0≤N≤106 ). In the following N lines, the i-th line contains two integers c1 and c2, which means that the member entity with ID i is partitioned into cluster c1 and cluster c2 by the old algorithm and the new algorithm respectively. The cluster IDs c1 and c2 can always fit into a 32-bit signed integer.

Output

For each test case, output a single line consisting of “Case #X: A B C”. X is the test case number starting from 1. A, B, and C are the numbers of splits, merges, and 1:1s.

Sample Input

2 3 0 0 0 0 0 1 4 0 0 0 0 1 1 1 1

Sample Output

Case #1: 1 0 0 Case #2: 0 0 2

Source

2015 ACM/ICPC Asia Regional Hefei Online

这题题意有点难懂，但是其实不难。要找出一对多，多对一，以及一对一的有多少。可以看成两个图。从一的那一侧把所有点找出来，然后在另外一侧对每个点关联的点，只要总度数一样就可以的。我写暴力了，vector 导致了MLE。然后上邻接表，然后AC。

/* ***
Author :kuangbin
Created Time :2015/9/27 14:13:19
File Name :F:\ACM\2015ACM\2015ÍøÂçÈü\2015ºÏ·Ê\1003.cpp
************************************************ */

#include <stdio.h>

#include <string.h>

#include

#include <math.h>

#include <stdlib.h>

#include <time.h>
using namespace std;

const int MAXN = 1000010;
int a[MAXN],b[MAXN];
int tot;
bool used[MAXN];

struct Vec {
struct Node {
int to,next;
}node[MAXN];
int head[MAXN],tot;
int size[MAXN];
void init() {
tot = 0;
memset(head,-1,sizeof(head));
memset(size,0,sizeof(size));
}
void Add(int i,int v) {
node[tot].to = v;
node[tot].next = head[i];
head[i] = tot++;
size[i]++;
}
}V1,V2;

int main()
{
int T;
int n;
scanf(“%d”,&T);
int iCase = 0;
while(T–) {
iCase++;
scanf(“%d”,&n);
map<int,int>mp1,mp2;
int tot1 = 0;
int tot2 = 0;
mp1.clear();
mp2.clear();
V1.init();
V2.init();
for(int i = 0;i < n;i++) {
scanf(“%d%d”,&a[i],&b[i]);
if(mp1.find(a[i]) == mp1.end()) {
mp1[a[i]] = tot1++;
}
if(mp2.find(b[i]) == mp2.end()) {
mp2[b[i]] = tot2++;
}
a[i] = mp1[a[i]];
b[i] = mp2[b[i]];
V1.Add(a[i],i);
V2.Add(b[i],i);
}
int ans1 = 0;
int ans2 = 0;
int ans3 = 0;
memset(used,false,sizeof(used));
for(int i = 0;i < tot1;i++) {
if(V1.size[i] < 1)continue;
int cnt = 0;
int num = 0;
for(int j = V1.head[i]; j != -1;j = V1.node[j].next) {
int v = V1.node[j].to;
if(!used[b[v]]) {
cnt += V2.size[b[v]];
used[b[v]] = true;
num++;
}
}
if(cnt == V1.size[i] && num > 1)ans1++;
if(cnt == V1.size[i] && num == 1)ans3++;
for(int j = V1.head[i]; j != -1;j = V1.node[j].next) {
int v = V1.node[j].to;
used[b[v]] = false;
}
}
for(int i = 0;i < tot2;i++) {
if(V2.size[i] < 1)continue;
int cnt = 0;
int num = 0;
for(int j = V2.head[i]; j != -1;j = V2.node[j].next) {
int v = V2.node[j].to;
if(!used[a[v]]) {
cnt += V1.size[a[v]];
used[a[v]] = true;
num++;
}
}
if(cnt == V2.size[i] && num > 1)ans2++;
for(int j = V2.head[i]; j != -1;j = V2.node[j].next) {
int v = V2.node[j].to;
used[a[v]] = false;
}
}
printf(“Case #%d: %d %d %d\n”,iCase,ans1,ans2,ans3);
}

return 0;

}